By Paul David Flood
When Danish composer Per Nørgård discovered the art of the schizophrenic Swiss painter Adolf Wölfli at an outsider art exhibit in 1979, he was struck by the fractal construction of these paintings and their similarity to his infinity series, a compositional system based on an integer sequence which he claimed to have “discovered” and used in his works throughout his “hierarchical period” of the 1960s and 70s.<1> Nørgård’s study of Wölfli’s tormented life influenced his subsequent compositional output during the early 1980s, sonically framing his existential crisis of how his “ideal” world may be envisioned.<2> At the heart of these works is the notion of conflict between “idyll and catastrophe” within the human experience; the apperception of unhappiness as a necessary part of experiencing happiness.<3> This essay suggests how Nørgård’s crisis manifested in his compositional technique by analyzing his unconventional use of the infinity series in his first work inspired by Wölfli, Wie Ein Kind.

Adolf Wölfli, General view of the island Neveranger, 1911.
Written between 1979 and 1980 on a commission from the Nordiska Körkomittén, Wie Ein Kind frames conflict through its exploration of childlike experiences.<4> The first and third movements, “Wiigen-Lied” and “Trauermarsch mit einem Unglücksfall,” bear motivic similarities and set a nonsense text written by Wölfli. In the first movement, the soloist’s wails and distant cries evoke the image of a street vendor, or a mother calling to her child from a tower. In the third movement, the soloist attempts to conform with the choir but suffers from an embarrassing stutter which keeps them rhythmically misaligned with the choir. The second movement stands in contrast to its bookending movements. Set to Rainer Marie Rilke’s “Frühlings-Lied,” the movement’s harmonic simplicity and playful texture depicts childlike joy and sensual awareness.<5> A later section of this movement employs a reduced form of Nørgård’s infinity series called the two-tone infinity series. As Wie Ein Kind is the first piece written in the Wölfli period of Nørgård’s oeuvre, Nørgård’s reduction of his own technique signifies the manifestation of his crisis in his composition.
The infinity series is a recursive integer sequence built upon the outward projection of intervals, in both directions, beginning from the very first interval of a given row, counted in semitones.<6> This process of intervallic projection can also be used to reduce an infinity series into a two-tone infinity series. I will introduce the infinity series, demonstrate how Nørgård may have reduced his original series into a two-tone infinity series, and discuss the two-tone infinity series within mm. 98-129 of “Frühlings-Lied.” (Note that measure numbers referenced in this essay align to the score which has been made commercially available by Edition Wilhelm Hansen.<10>) These measures contain four units with similar motives in the tenor and alto voices that are constructed by the two-tone infinity series. Each successive unit is varied from its predecessor in texture, pitch collection, and rhythm of the outer voices.




Figure 1: Nørgård, “Frühlings-Lied,” mm. 97-132. Annotated to show beginnings of each unit.
Figure 2 is an infinity row based on the ascent of two semitones from the starting pitch C. This series will be called Inf. C+2, indicating the starting pitch and the respective ordered pitch interval.
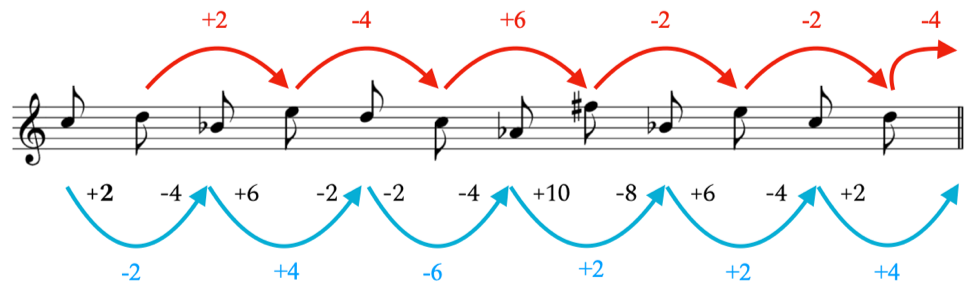
Figure 2: The first twelve pitches of Inf. C+2.
The aforementioned process of constructing an infinity series is one in which the ordered pitch intervals from one note to the next are projected to determine the succeeding pitches in a series. Starting from the beginning of the series, the interval of two rising semitones between C to D will determine the following two pitches. The projection of intervals occurs in such a way that every other note is related, as shown by the blue and red arrows in Figure 2. Each interval projects two notes in opposite directions: the first note to be projected will move in relation to the starting pitch, but in the opposite direction of the interval being projected . In other words, the ascent of two semitones between C and D will project a descent of two semitones between C and the Bb after the D. The next note will be projecte d in the same direction as the interval between C and D, but will do so in relation to the D. The ascent of two semitones from C to D will project the same interval between D and the E after Bb. Therefore, in the context of Inf. C+2, the two-semitone ascent from C to D will project itself such that the third note of the series will move two semitones below C, to Bb, and the fourth note of the series will move two semitones above D, to E. The series then continues with the interval between D and Bb, a descent of four semitones, leading to D and C as the next two pitches in the serie The process continues toward infinity (or at least where the composer decides to stop).<7>
In Wie Ein Kind, Nørgård uses what is called a two-tone infinity series, a reduced form of the infinity series which contains and repeats the same two pitches which began the original infinity series. The repetitive ordering of these two pitches can be identified through the very process of reduction. To convert Inf. C+2 into a two-tone infinity series, we consider the pitches C and D as numerical values 0 and 1. Each successive pitch will be given a value in relation to the starting pitch; Bb is -1, E is 2, Ab is -2, and so on (these values are given based on the number of whole steps above or below C).<8> Each value will then be added to or subtracted from by a multiple of 2 until it becomes either value 0 or 1, as demonstrated by the blue numbers in Figure 3. If the value is above 1, it will be subtracted by a multiple of 2, and if the value is below 0, it will be added to by a multiple of 2.<9>

Figure 3: Process of reduction from Inf. C+2 to 2TInf. C+2.
Given the above examples, provided for technical context, I now turn to the two-tone infinity series that is present in “Frühlings-Lied.” Between measures 98 and 129 are four units based on the two-tone infinity series. Nørgård se ts a larger two-tone infinity series as the basis of these units, including only the consecutively repeating pitches within that series in these units to create what he calls a “pishop” rhythm . A pishop rhythm is the extraction and tying-together of these consecutively repeating pitches from their larger two-tone series. Repeated notes from the larger series are converted into tied notes in the score, creating the pishop rhythm. Pitches that do not have a repetition before or after themselves are replaced by a rest, as shown in the Figures 4.1 and 4.2 in which the pishop rhythm in the tenor line is isolated to reveal the series 2TInf. E-9.

Figure 4.1: Nørgård, “Frühlings-Lied,” mm. 98-105, tenor.

Figure 4.2: Conversion between tenor pishop rhythm and 2TInf. E-9.
At first glance, there may appear to be discrepancies in this conversion, but these are intentional and unique to each unit. For example, the pishop rhythm containing an eighth note tied to a quarter note is most likely a textural choice, as it is not an indication that three consecutively repeated pitches exist in the two-tone infinity series (this would not be possible based on the process of reduction). In addition, the large distance between the two pitches of the series used in “Frühlings-Lied” means that neither pitch can be identified with values 0 or 1 as in the technical example above. Nørgård’s use of the two-tone infinity series in other works does allow for this identification of numerical value, and even though the series in question does not possess this quality, it is still considered a two-tone infinity series for functional purposes.<11> Nørgård’s use of a two-tone infinity series that is non-derivative is perhaps another manifestation of his crisis and the transition into his Wölfli period.
The introductory unit in mm. 98-105 features two infinity rows in the inner voices while the basses sing in fifths below. The second unit in mm. 106-113 features variation in the outer voices while the content in the inner voices remains the same. Here, the soprano part enters above while the fifths in the bass move by glissandi. The third unit in mm. 114-121 sees multiple variations. First, the soprano line from the previous unit does not return. There is an additional pitch B added to the tenor line. A possible explanation for the addition of this pitch is to align with the first bass’ Bs on m. 115 and m. 116. The most important variation here is disruption of the pishop rhythm at the end of measure 116, where the rhythmic values proceed from quarter note on G, to eighth note on E, to half note on G, rather than three consecutive occurrences of two tied eighth notes. In addition, the alto and tenor parts fall out of alignment for a brief moment in measure 116, where the alto sings an eighth note on beat two but the tenor holds on for a bit longer with a quarter note. The fourth and final unit in mm. 122-129 sees the return of the soprano line with shorter durations of the material from unit two, and the removal of the glissandi from the bass. At the beginning of this unit, the tenor briefly sings a unison D with the alto. This culminating two-tone unit presents slightly obscured inner voice lines, informed by the two-tone infinity series, with motives in the outer voices to provide accompanying texture.
Nørgård’s use of his infinity series in its reduced, non-derivative form harkens as a point of no return, a glimpse into something that once was but which cannot be revived in its original form. Much in the same way, Nørgård’s study of Wölfli challenged his former vision of the ideal world to accommodate outsiders such as Wölfli. <12> Nørgård did not necessarily intend for this music to be ekphrastic in its content — that is, he did not attempt to illustrate any particular artwork through musical composition. Instead, the Wölfli works originate from Nørgård’s desire to situate himself as a medium through which the “cries and phantasms of a lonely person, afflicted for decades, who suddenly demanded entry into Per Nørgård’s music” could be heard.<13> Wie Ein Kind frames Nørgård’s struggle to abandon his fixation for order in favor of the opportunities presented by chaos: to embrace the outsider, Wölfli, in his shifting ideology and compositional style over the next few years.
ENDNOTES
<1> Erling Kullberg, “Beyond Infinity: On the infinity series — the DNA of hierarchical music,” in The Music of Per Nørgård: Fourteen Interpretive Essays, ed. Anders Beyer (Brookfield, VT: Ashgate Publishing Co., 1996), 71.
<2> Jean Christensen, “Part I—New Music in Denmark” in New Music of the Nordic Countries, ed. John D. White (Hillsdale, NY: Pendragon Press, 2002), 41.
<3> Erling Kullberg, “Wie Ein Kind for choir a capella,” https://web.archive.org/web/20070522153323/http://www.pernoergaard.dk/eng/udvalgte/167.html.
<4> Kullberg, “Wie Ein Kind.”
<5> Per Nørgård, Wie Ein Kind (Copenhagen: Edition Wilhelm Hansen, 1996), iii.
<6> For a mathematical explanation of the infinity series, see the entry on the Thue-Morse Sequence in the On-Line Encyclopedia of Integer Sequences: https://oeis.org/search?q=thue-morse&sort=&language=english&go=Search.
<7> Jørgen Mortensen, “Construction by the projection of intervals,” https://web.archive.org/web/20070523051434/http://www.pernoergaard.dk/eng/strukturer/uendelig/ukonstruktion01.html
<8> Note that these values are not to be confused with pitch class set theory, in which C is also 0 but D is 2.
<9> Jørgen Mortensen, “An infinity series with only 4 or 2 different variants,” https://web.archive.org/web/20070522153340/http://www.pernoergaard.dk/eng/strukturer/uendelig/u4.html.
<10> The score for Wie Ein Kind is available for purchase at: https://www.wisemusicclassical.com/work/21767/Wie-ein-Kind–Per-N%C3%B8rg%C3%A5rd/.
<11> Kullberg, “Wie Ein Kind.”
<12> Christensen, 42.
<13> Jørgen I. Jensen, “The Great Change: Per Nørgård and Adolf Wölfli” in The Music of Per Nørgård: Fourteen Interpretive Essays, ed. Anders Beyer (Brookfield, VT: Ashgate Publishing Co, 1996), 9.

Paul David Flood is pursuing his Master’s degree in Musicology at the University of California, Irvine. His research focuses on developments of Nordic musical identity and modernism in Denmark. He is currently working on his Master’s thesis, titled “Embracing the Outsider: Framing Conflict in Per Nørgård’s Wölfli Works.” Additional interests also include contemporary music reception, music and philosophy, vocal literature, and the Eurovision Song Contest. He received his B.A. in Music from Westminster Choir College in 2019 and is an active choral singer.
